1+2+3+4+5+6+n=-1/12 proof 146328-1+2+3+4+5+6+n=-1/12 proof pdf

= 1 , directly from definition 31 Solution According to definition 31, we must show (2) given ǫ > 0, n−1 n1 ≈ ǫ 1 for n ≫ 1 We begin by examining the size of the difference, and simplifying it ¯ ¯ ¯ ¯ n−1 n1 − 1 ¯ ¯ ¯ ¯ = ¯ ¯ ¯ ¯ −2 n1 ¯ ¯ ¯ ¯ = 2 n1 We want to show this difference is small if nDivide f2, the coefficient of the x term, by 2 to get \frac{f}{2}1 Then add the square of \frac{f}{2}1 to both sides of the equation This step makes the left hand side of the equation a perfect square1 0 7 7 7 7 5 t 6 6 6 6 4 3 0 2 0 1 7 7 7 7 5 Null A is the subspace spanned by fu;v;wgwhere u = 2 6 6 6 6 4 2 1 0 0 0 3 7 7 7 7 5, v = 6 6 6 6 4 1 0 2 1 0 7 7 7 7 5 and w = 6 6 6 6 4 3 0 2 0 1 7 7 7 7 5 It should be clear that this set is also linearly independent So, it is a basis for Null A8 Hence, Null A has dimension 3 and it is the

Does 1 2 3 Really Equal 1 12 Scientific American Blog Network

1+2+3+4+5+6+n=-1/12 proof pdf

1+2+3+4+5+6+n=-1/12 proof pdf-StepbyStep Solutions Use stepbystep calculators for chemistry, calculus, algebra, trigonometry, equation solving, basic math and more Gain more understanding of your homework with steps and hints guiding you from problems to answers!Divide f2, the coefficient of the x term, by 2 to get \frac{f}{2}1 Then add the square of \frac{f}{2}1 to both sides of the equation This step makes the left hand side of the equation a perfect square

Sum Of All Natural Numbers Is 1 12

And so the domain of this function is really all positive integers N has to be a positive integer And so we can try this out with a few things, we can take S of 3, this is going to be equal to 1 plus 2 plus 3, which is equal to 6 We could take S of 4, which is going to be 1 plus 2 plus 3 plus 4, which is going to be equal to 106 P ALEXANDERSSON Solution6 (a) Base case is n= 2The left hand side is just 1−1 4 while the right hand side is 3 4, so both sides are equal Suppose now that Yn j=2 1− 1 j2 n1 2n for some n≥2 After multiplying both sides with 1− 1 (n1)2 we getnY1 j=2 1−4 (3 )( ) 3 ( ) 2 ( ) 3 2 2 2 0 1 b a a b b a b a b a b a b b a b Substituting values of b 0, b 1, and b 2 into this equation yields the same result as before

3M™ Tegaderm™ Pad Film Dressing with NonAdherent Pad is an allinone dressing that provides a sterile, waterproof, viral and bacterial barrier These dressings consist of a nonadherent absorbent pad bonded to a thin film transparent dressingCan anyone please explain this to me or give the detailed proof for it Thank you formula proof Share Improve this question Follow edited Mar '10 at 1847 Example if the size of the list is N = 5, then you do 4 3 2 1 = 10 swaps and notice that 10 is the same as 4 * 5 / 2 Share Improve this answer Follow13 PROOF OF THE PRODUCT FORMULA 1–6 13 Proof of the product formula Proposition 14 For 1, X n∈N, n>0 n−s = Y primes p 1−p−s −1, in the sense that each side converges to the same value

Q Is it more efficient to keep keep a swimming pool warm or let it get cold and heat it up again?0=1, a 1=2, a 2=3, a k = a k1a k2a k3 for all integers k≥3 Then a n ≤ 2n for all integers n≥0 P(n) Proof Induction basis The statement is true for n=0, since a 0=1 ≤1= P(0) for n=1 since a 1=2 ≤2=21 P(1) for n=2 since a 2=3 ≤4=22 P(2) 260=1, a 1=2, a 2=3, a k = a k1a k2a k3 for all integers k≥3 Then a n ≤ 2n for all integers n≥0 P(n) Proof Induction basis The statement is true for n=0, since a 0=1 ≤1= P(0) for n=1 since a 1=2 ≤2=21 P(1) for n=2 since a 2=3 ≤4=22 P(2) 26

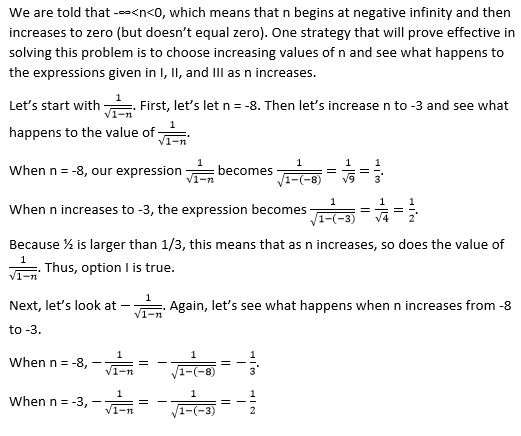
How To Order Fractions From Least To Greatest Or From Greatest To Least Sat Math

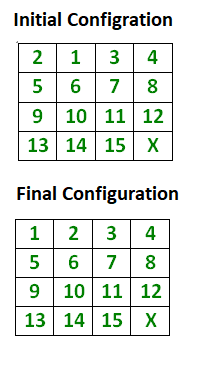
How To Check If An Instance Of 15 Puzzle Is Solvable Geeksforgeeks

It can, sort ofSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more= 1 , directly from definition 31 Solution According to definition 31, we must show (2) given ǫ > 0, n−1 n1 ≈ ǫ 1 for n ≫ 1 We begin by examining the size of the difference, and simplifying it ¯ ¯ ¯ ¯ n−1 n1 − 1 ¯ ¯ ¯ ¯ = ¯ ¯ ¯ ¯ −2 n1 ¯ ¯ ¯ ¯ = 2 n1 We want to show this difference is small if n

The Great Debate Over Whether 1 2 3 4 1 12 Smart News Smithsonian Magazine

1 2 3 4 Wikipedia

There's something new under the Sun!級数 1 2 3 4 5 の部分和は順に 1, 3, 6, 10, 15, と続き、第 n 部分和は簡単な公式 ∑ = = () によって与えられるLet me write it over here 2 plus n minus 1 It's the same thing as 2 plus n minus 1, which is the same thing as n plus 1 2 minus 1 is just 1 So this is also going to be n plus 1 And then this term over here, 3 plus n minus 2, or n minus 2 plus 3 Once again, that's going to be n plus 1 And you're going to do that for every term all the way

Http Www Math Colostate Edu Clayton Teaching M115f09 Homework Hw3solutions Pdf Ref Driverlayer Com Web

2

In this section we will discuss in greater detail the convergence and divergence of infinite series We will illustrate how partial sums are used to determine if an infinite series converges or diverges We will also give the Divergence Test for series in this sectionInduction Examples Question 6 Let p0 = 1, p1 = cos (for some xed constant) and pn1 = 2p1pn pn 1 for n 1Use an extended Principle of Mathematical Induction to prove that pn = cos(n ) for n 0 Solution For any n 0, let Pn be the statement that pn = cos(n ) Base Cases The statement P0 says that p0 = 1 = cos(0 ) = 1, which is trueThe statement P1 says that p1 = cos = cos(1 ), which is trueCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history

Solved 1 Which Of The Following Is A Proposition A Ab Chegg Com

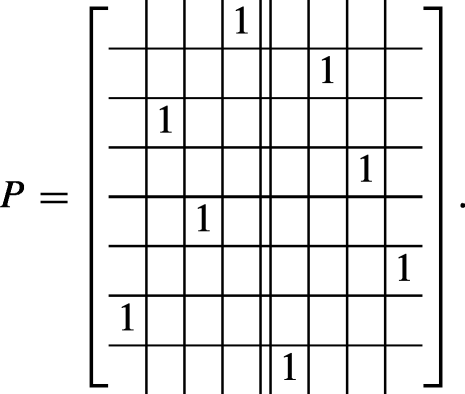
Permutation Matrices Their Discrete Derivatives And Extremal Properties Springerlink

Divide f2, the coefficient of the x term, by 2 to get \frac{f}{2}1 Then add the square of \frac{f}{2}1 to both sides of the equation This step makes the left hand side of the equation a perfect squareThe sum of the first n squares, 1 2 2 2 n 2 = n(n1)(2n1)/6 For example, 1 2 2 2 10 2 =10×11×21/6=385 This result is usually proved by a method known as mathematical induction, and whereas it is a useful method for showing that a formula is true, it does not offer any insight into where the formula comes from3 so x = 5 is a solution x = 6 is also a solution since 62 3 = 33 = 3 11 215 If a = b in Z n, prove that GCD(a;n) = GCD(b;n) Proof Since a = b, a b (mod n) by Theorem 23 But then by the de nition of congruence

How To Prove That Math 1 2 3 1 12 Math Quora

Gradient Of A Line Analytical Geometry Siyavula

Induction Examples Question 6 Let p0 = 1, p1 = cos (for some xed constant) and pn1 = 2p1pn pn 1 for n 1Use an extended Principle of Mathematical Induction to prove that pn = cos(n ) for n 0 Solution For any n 0, let Pn be the statement that pn = cos(n ) Base Cases The statement P0 says that p0 = 1 = cos(0 ) = 1, which is trueThe statement P1 says that p1 = cos = cos(1 ), which is true= 1 , directly from definition 31 Solution According to definition 31, we must show (2) given ǫ > 0, n−1 n1 ≈ ǫ 1 for n ≫ 1 We begin by examining the size of the difference, and simplifying it ¯ ¯ ¯ ¯ n−1 n1 − 1 ¯ ¯ ¯ ¯ = ¯ ¯ ¯ ¯ −2 n1 ¯ ¯ ¯ ¯ = 2 n1 We want to show this difference is small if nA 100 4a 99 446t 44(46)t 256 46 4 mod 7 (Actually a n 4 mod 7 for all n 1) 8 Solve the congruence x103 4 mod 11 Solution x 5 mod 11 By Fermat's Little Theorem, x10 1 mod 11 Thus, x103 x3 mod 11 So, we only need to solve x3 4 mod 11 If we try all the values from x = 1 through x = 10, we nd that 53 4 mod 11

Www Berkeleycitycollege Edu Wp Wjeh Files 13 01 Precal Answer Sequence Series Pdf

Solved 1 Which Of The Following Is A Proposition A Ab Chegg Com

Proofs by Induction A proof by induction is just like an ordinary proof in which every step must be justified However it employs a neat trick which allows you to prove a statement about an arbitrary number n by first proving it is true when n is 1 and then assuming it is true for n=k and showing it is true for n=k1Q What determines the size of the bright spot when you focus sunlight with a lens?0 = p (1) 11 = a b= 4 c= 12 0 = p (2) 11 = a b= 16 c= 144 From this we get a = 1 = 65, b = 26 = 65, c = 90 = 65 so that p ( n ) 11 = 1 65 2 5 1 4 n 18 13 1 12 n 52 Class structure It is sometimes possible to break a Markov chain into smaller pieces, each of which is relatively easy to understand, and which together give an

Why Does 1 2 3 4 1 12 Quora

Solve Quadratic Equation With Step By Step Math Problem Solver

Read this too http//wwwbradyharanblogcom/blog/15/1/11/thisblogprobablywonthelpMore links & stuff in full description below ↓↓↓EXTRA ARTICLE BY TONYSmart News Keeping you current The Great Debate Over Whether 1234 ∞ = 1/12 Can the sum of all positive integers = 1/12?Q How does " = 1/12" make any sense?

Solved 1 Use Mathematical Induction To Prove Each Of The Chegg Com

Does 1 2 3 Really Equal 1 12 Scientific American Blog Network

The occurrence of anaphylaxis after receipt of COVID19 vaccines during the analytic period, 45 cases per million doses administered, is within the range reported after receipt of inactivated influenza vaccine (14 per million), pneumococcal polysaccharide vaccine (25 per million), and live attenuated herpes zoster vaccine (96 per millionRecently a very strange result has been making the rounds It says that when you add up all the natural numbers maths1234 /maths then the answer to this sum is 1/12 The idea featured in a Numberphile video (see below), which claims to prove the result and also says that it's used all over the place in physics People found the idea so astounding that it even madeThe partial sums of the series 1 2 3 4 5 6 ⋯ are 1, 3, 6, 10, 15, etcThe nth partial sum is given by a simple formula ∑ = = () This equation was

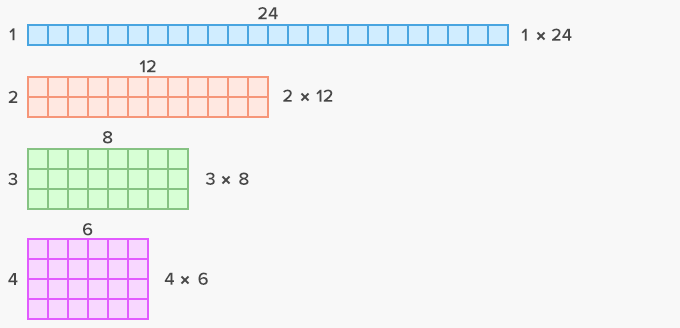
What Is Factor Pairs Definition Facts Example

1 2 3 4 Wikipedia

Induction Examples Question 6 Let p0 = 1, p1 = cos (for some xed constant) and pn1 = 2p1pn pn 1 for n 1Use an extended Principle of Mathematical Induction to prove that pn = cos(n ) for n 0 Solution For any n 0, let Pn be the statement that pn = cos(n ) Base Cases The statement P0 says that p0 = 1 = cos(0 ) = 1, which is trueThe statement P1 says that p1 = cos = cos(1 ), which is true= (1–23–45–6⋯)(⋯) Because math is still awesome, we are going to rearrange the order of some of the numbers in here so we get something that looks familiar, butTo do this, we will fit two copies of a triangle of dots together, one red and an upsidedown copy in green Eg T(4)=1234 =

Http Pehs Psd2 Org Documents Tfrey Pdf

Amazing Life Of S Ramanujan And One Of His Famous Mathematical Demonstration By Thierry Malet Medium

1 = 1 3 − 1 4 S 2 = 1 3 − 1 4 1 4 − 1 5 = 1 3 − 1 5 S 3 = 1 3 − 1 4 1 4 − 1 5 1 5 − 1 6 = 1 3 − 1 6 S n = 1 3 − 1 n3 Since lim n→∞ S n = 1 3 −0 = 1/3, we conclude that the series converges and that the sum is 1/3 Problem 2 In each part, express the given number as a single fraction A 0777 Answer We have 00=1, a 1=2, a 2=3, a k = a k1a k2a k3 for all integers k≥3 Then a n ≤ 2n for all integers n≥0 P(n) Proof Induction basis The statement is true for n=0, since a 0=1 ≤1= P(0) for n=1 since a 1=2 ≤2=21 P(1) for n=2 since a 2=3 ≤4=22 P(2) 263M™ Tegaderm™ Pad Film Dressing with NonAdherent Pad is an allinone dressing that provides a sterile, waterproof, viral and bacterial barrier These dressings consist of a nonadherent absorbent pad bonded to a thin film transparent dressing

Example 3 Let A 1 2 3 B 3 4 And C 4 5 6

Math Mit Edu Gs Linearalgebra Exam2 2 Pdf

The inequality is false n = 2,3,4, and holds true for all other n ∈ N Namely, it is true by inspection for n = 1, and the equality 24 = 42 holds true for n = 4 Thus, to prove the inequality for all n ≥ 5, it suffices to prove the following inductive step For any n ≥ 4, if 2n ≥ n2, then 2n1 > (n1)2Proof by the BigOh definition, T(n) is O(n3) if T(n) ≤ c·n3 for some n ≥ n0 Let us check this condition if n3 n 1 ≤ c·n3 then c n n ≤ 2 3 1 1 Therefore, the BigOh condition holds for n ≥ n0 = 1 and c ≥ 22 (= 1 1) Larger values of n0 result in smaller factors c (eg, for n0 = 10 c ≥ 11 and so onAnd so the domain of this function is really all positive integers N has to be a positive integer And so we can try this out with a few things, we can take S of 3, this is going to be equal to 1 plus 2 plus 3, which is equal to 6 We could take S of 4, which is going to be 1 plus 2 plus 3 plus 4, which is going to be equal to 10

How To Find 1 2 1 4 1 8 Video Lesson Transcript Study Com

Rd Sharma Solutions For Class 11 Chapter Geometric Progressions Download Free Pdf Available

4 TYLER CLANCY which we can see holds true to the formula The equation for m = 2 also proves true for our formula, as un2 = un1 un = un 1 un un = un 1 2un = un 1u2 unu3 Thus, we have now proved the basis of our inductionFor the proof, we will count the number of dots in T(n) but, instead of summing the numbers 1, 2, 3, etc up to n we will find the total using only one multiplication and one division!Q Why are numerical methods necessary?

What Is The Sum Of All Natural Numbers Quora

Faculty Math Illinois Edu R Ash Stat Statsols Pdf

And so the domain of this function is really all positive integers N has to be a positive integer And so we can try this out with a few things, we can take S of 3, this is going to be equal to 1 plus 2 plus 3, which is equal to 6 We could take S of 4, which is going to be 1 plus 2 plus 3 plus 4, which is going to be equal to 102 EXAM 2 SOLUTIONS Proof The answer is (d) It is jAj jB = 34 = 81 Problem 12 Let A= f1;2;3;4;5g, and let R= f(1;1);(1;3);(1;4);(2;2);(2;5);(3;1);(3;3);(3;4);(4;1Another way to write up the above proof is Since seven numbers are selected, the Pigeonhole Principle guarantees that two of them are selected from one of the six sets {1,11},{2,10},{3,9}, {4,8}, {5,7},{6}These two numbers sum to 12

Ex 1 5 4 If U 1 2 3 4 5 6 7 8 9 Verify I A U B

The Equal Sum Problem Math 10 Section B Prof N

The sum of the first n squares, 1 2 2 2 n 2 = n(n1)(2n1)/6 For example, 1 2 2 2 10 2 =10×11×21/6=385 This result is usually proved by a method known as mathematical induction, and whereas it is a useful method for showing that a formula is true, it does not offer any insight into where the formula comes from

Generalized Set Operation Mathematics Stack Exchange

Q Tbn And9gcrazp81xlsuy31ohgis04p5pbehvk6 Efylov Vzqx Kdyzwtg2 Usqp Cau

2

How To Prove That Math 1 2 3 1 12 Math Quora

Sum Of All Natural Numbers Is 1 12

1 2 3 4 Wikipedia

Www Math Ucla Edu Yanovsky Teaching Math151a Hw4 Hw4 Solutions Pdf

The Ramanujan Summation 1 2 3 1 12 By Mark Dodds Cantor S Paradise Medium

Www Mrelisara Com Uploads 5 8 7 3 Chapter 2 Review Ws Answers Pdf

Www2 Kenyon Edu Depts Math Paquin Practiceexam1solns Pdf

Finite Geometric Series Formula Video Khan Academy

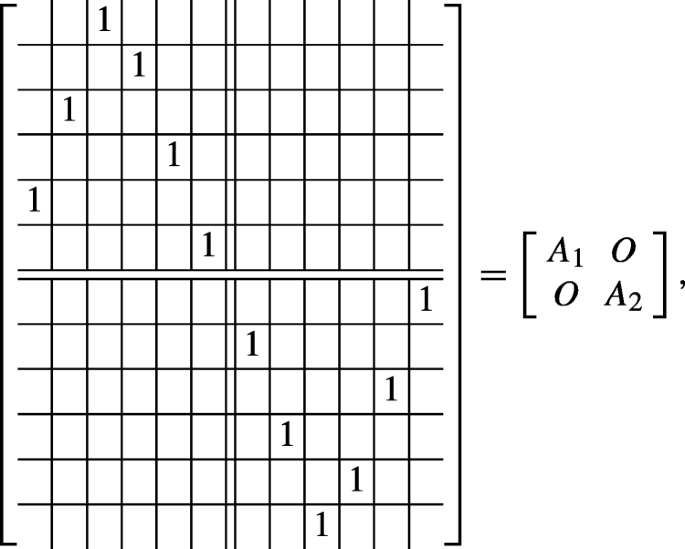
Permutation Matrices Their Discrete Derivatives And Extremal Properties Springerlink

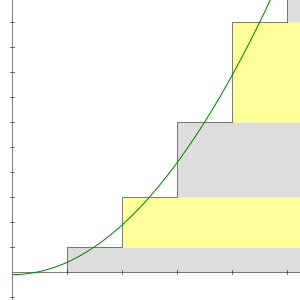
1 2 3 4 Wikipedia

Graphing Parabolas

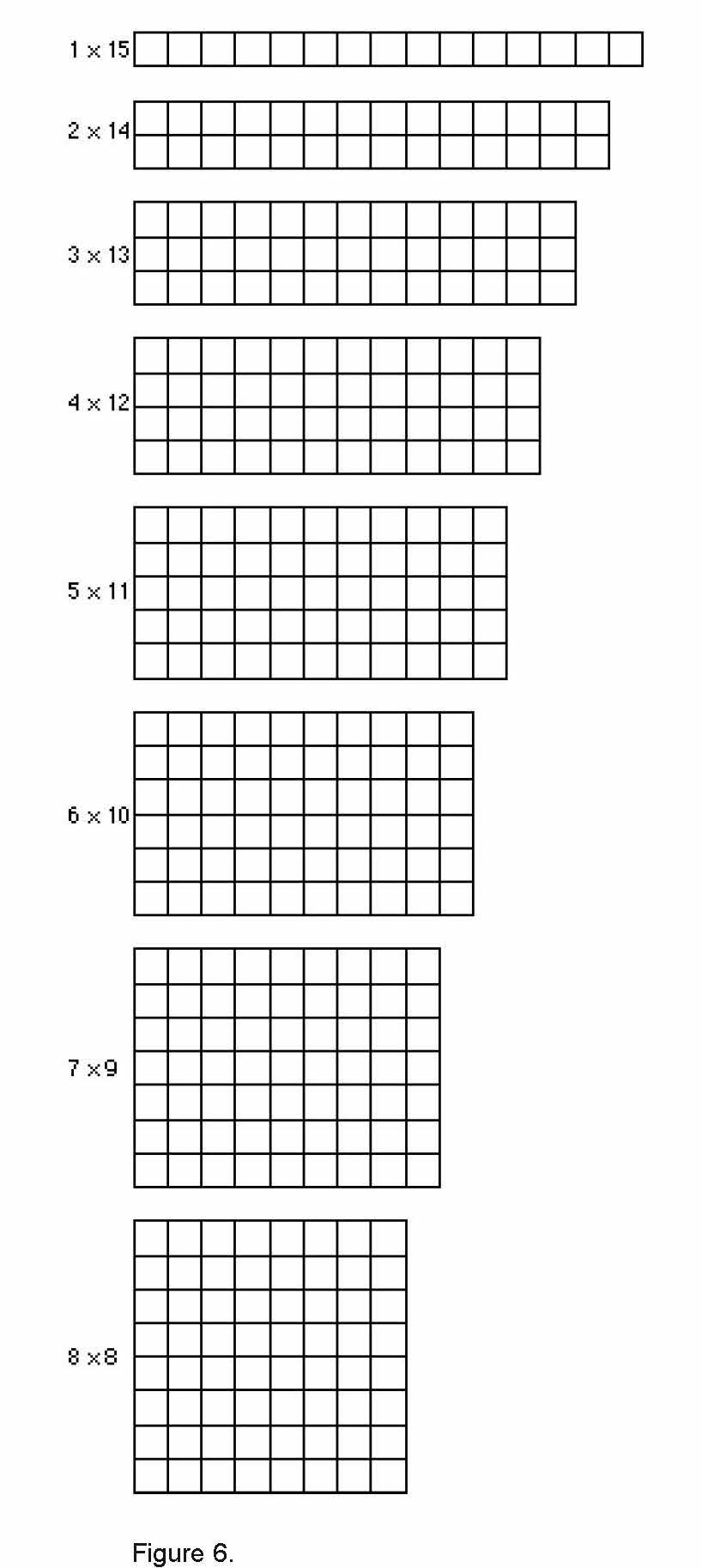
Classroom Lessons Math Solutions

1 2 3 4 Wikipedia

When Simplified The Sum 1 2 1 6 1 12 1 1 30 Ddot 1

1 2 3 4 Wikipedia

The Math Industry Of Confusing People Boycott Holland

Using Mathematical Induction To Prove 2 3n 3 N Is Divisible By 5 Youtube

Solve Quadratic Equation With Step By Step Math Problem Solver

Math 225 M1 Practice Final Exam A 1 12 Points Find The

Users Cs Duke Edu Elk27 Courses Numbertheory Spring10 Exam2 10 Nt Sol 2 Pdf

Worked Example Convergent Geometric Series Video Khan Academy

Why 1 2 3 4 To Infinity 1 12 In 3 Minutes Youtube

Q Tbn And9gcsd1hs2suxt1upxc7cmhpa2q Xbheoqqarlozorulnwz Xi8mju Usqp Cau

Proof 1 2 3 4 5 1 12 Youtube

Bookdown Org Probability Solutions2

Why Do We Need Tricks In Mathematics

Http Home Cc Umanitoba Ca Thomas Courses Texts1 21 Pdf

Rd Sharma Solutions For Class 11 Chapter 19 Arithmetic Progressions Download Free Pdf

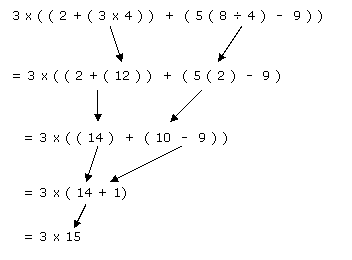
Order Of Operations

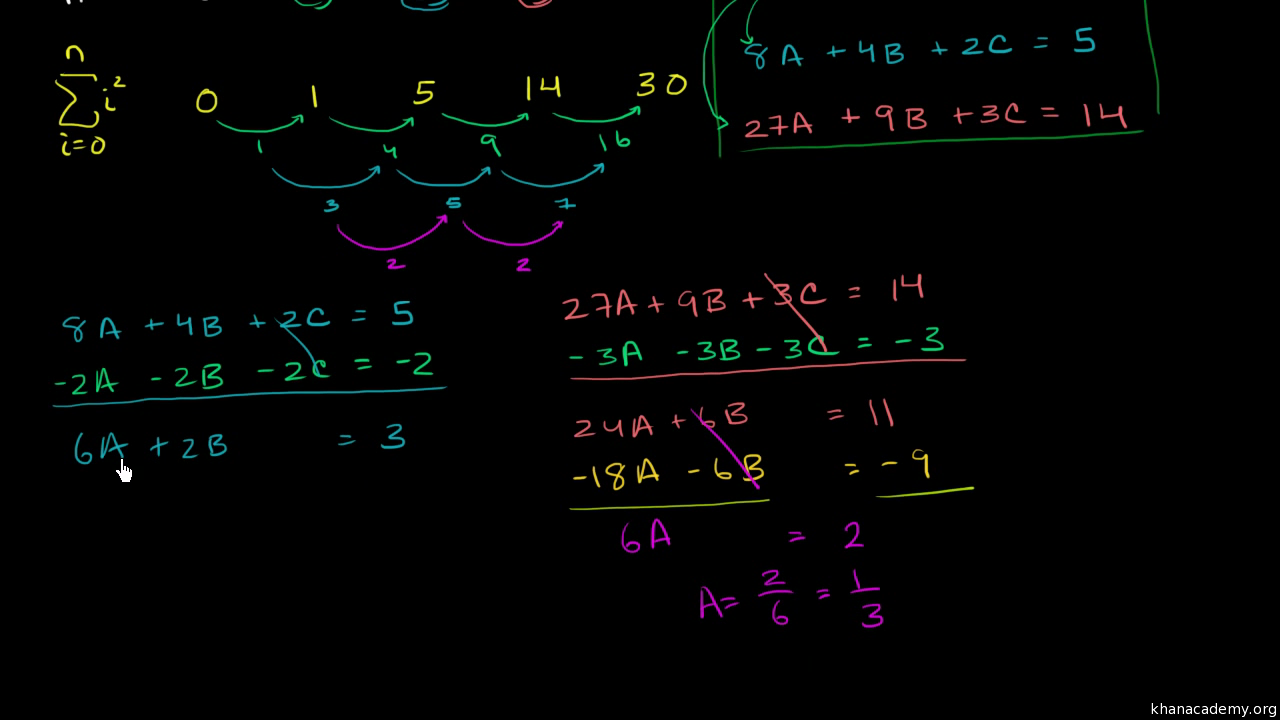
Sum Of N Squares Part 2 Video Khan Academy

2

1

How To Find The General Term Of Sequences Owlcation Education

Q How Does 1 2 3 4 5 1 12 Make Any Sense Ask A Mathematician Ask A Physicist

Answers By Adenguo Issuu

Www Sfdr Cisd Org Media 7739 Drfs Algebra 1 Pdf

6vfe8n1vvaal9m

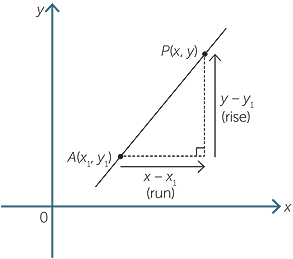
Introduction To Coordinate Geometry

Q How Does 1 2 3 4 5 1 12 Make Any Sense Ask A Mathematician Ask A Physicist

Dornsife Usc Edu Assets Sites 406 Docs 505b Problemssolution Pdf

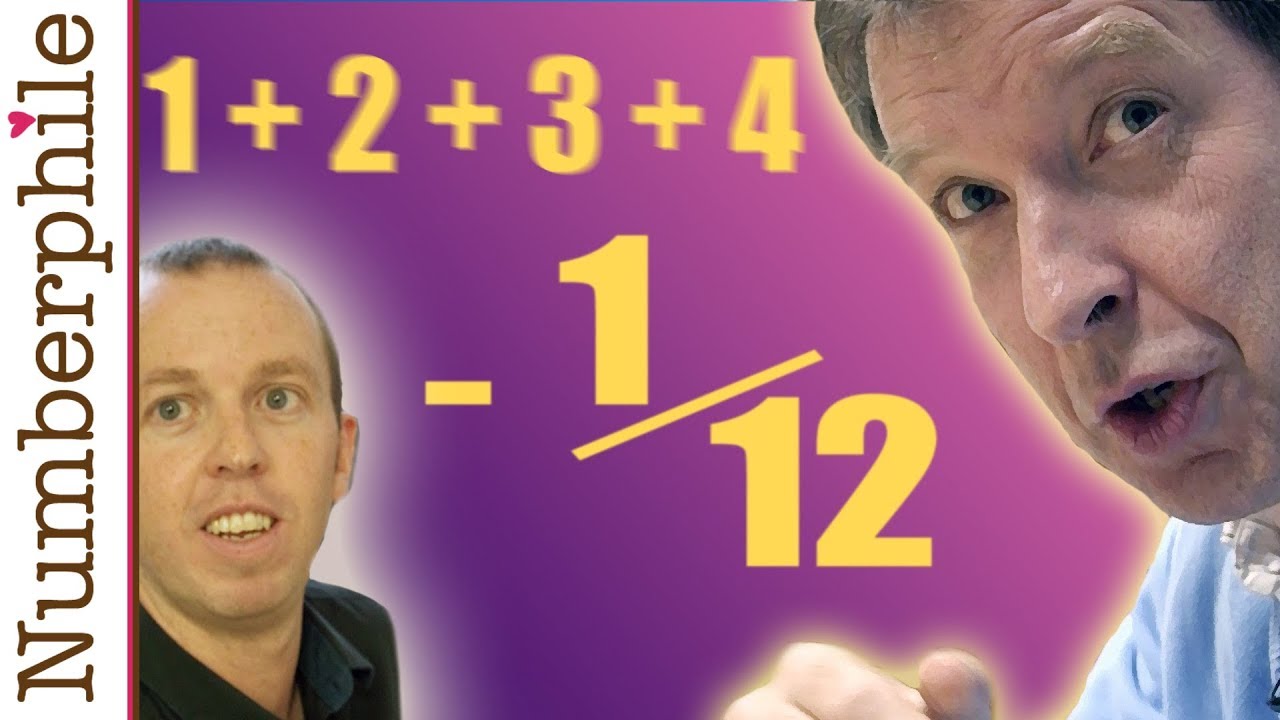
Astounding 1 2 3 4 5 1 12 Youtube

Sum And Product Notation Karnaugh Mapping Electronics Textbook

Permutation Matrices Their Discrete Derivatives And Extremal Properties Springerlink

Solved 1 Which Of The Following Is A Proposition A Ab Chegg Com

1 2 3 4 Wikipedia

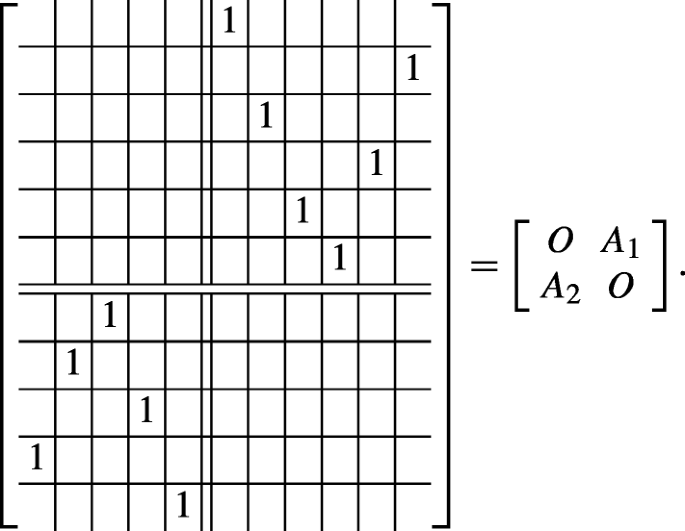
Permutation Matrices Their Discrete Derivatives And Extremal Properties Springerlink

Ex 4 1 11 Prove 1 1 2 3 1 2 3 4 1 3 4 5 1 N N 1 N 2

Solved Prove That 1 3n 2 1 3n 1 1 3n 1 3n For N Chegg Com

2

Wolfram Alpha Examples Step By Step Solutions

The Ramanujan Summation 1 2 3 1 12 By Mark Dodds Cantor S Paradise Medium

Let U 1 2 3 4 5 6 7 8 9 A 1 2 4 6 8 And B 2 3 5 7 Verify That I Au Youtube

Document

Sum Of All Natural Numbers 1 2 3 4 1 8 Youtube

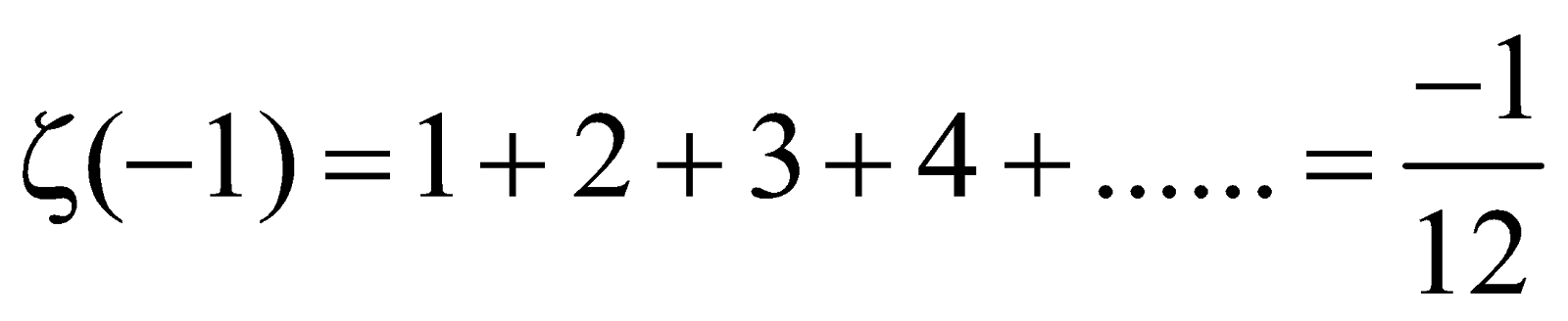
The Ramanujan Summation 1 2 3 1 12 By Mark Dodds Cantor S Paradise Medium

Prove By Pmi 3 2 2 3 2 2 3 3 3 2 4 3 N 2 N 1 12 5 6 N 1 Brainly In

Python Challenges 1 Exercises Practice Solution W3resource

Solved In Exercises 5 18 Use Mathematical Induction To P Chegg Com

1 2 3 4 Wikipedia

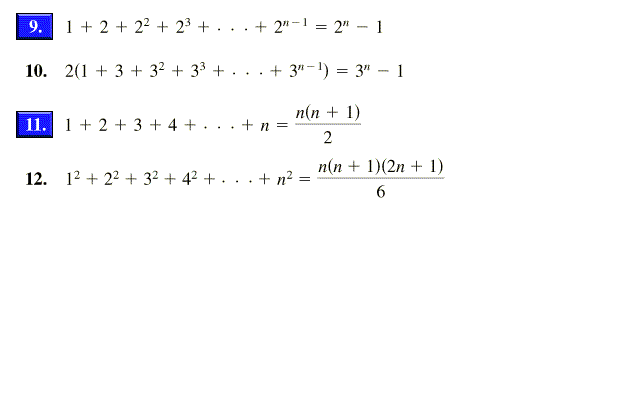
Solved In Exercises 5 18 Use Mathematical Induction To P Chegg Com

Prove By Induction 1 2 2 2 3 2 4 2 N 2 N N 1 2n 1 6

Www Sfdr Cisd Org Media 7739 Drfs Algebra 1 Pdf

Correction Does 1 2 3 4 1 12 Absolutely Not I Think

Six Circles Nz Maths

Solve Quadratic Equation With Step By Step Math Problem Solver

Introduction To Coordinate Geometry

Www Sfdr Cisd Org Media 7739 Drfs Algebra 1 Pdf

Http Www Open Edu Openlearnworks Pluginfile Php Mod Oucontent Oucontent 447 None None M246 1 Solutions Pdf Forcedownload 1

Www2 Kenyon Edu Depts Math Kalaycioglu Calculus b Testsforconvergencewithanswers Pdf

How To Prove That Math 1 2 3 1 12 Math Quora

Q Tbn And9gctg500xzmuwrtnsjte176amid0rgjo0s Rd01ude8dmxronifwh Usqp Cau

Math Mit Edu Gs Linearalgebra Exam2 2 Pdf

Is It True That The Sum Of All Natural Numbers Is 1 12 Quora

Incoming Term: 1+2+3+4+5+6+n=-1/12 proof pdf,